The Bias-Variance Tradeoff

The Setup

One of the most fundamental skills in Artificial Intelligence and Machine Learning modeling is understanding what causes your model to make erroneous predictions. To make as accurate predictions as we can, we must reduce our model’s error rate and doing so requires a firm understanding of what statisticians call The Bias-Variance Tradeoff.

How well does your model predict when you test it with new data? There are three potential sources of model error:

Total Error = Variance + Bias^2 + Noise

Since bias and variance describe competing problems with your modeling procedure, you need to know which is the source of your model’s high error rate, otherwise you risk exacerbating the issue.

Once you understand what the tradeoff between bias and variance means for the underfitness or overfitness of your model, you can employ the appropriate method to minimize your model’s rate of error and make better predictions.

Definitions

Variance - The squared difference between test values and the expected (model) values. How far off was our expectation from reality? High variance between test data and model output is a sign the model is overfit to the training data.

Variance = (Test Value - Expected Value)^2

Bias - Error of a given model because the model implements, and is biased toward, a particular kind of solution, e.g. a Linear Classifier. This model bias is inherent to the model solution and cannot be overcome by training with more or different data. High bias is a sign the model is underfit to the training data.

Noise - Irreducible error inherent to the dataset. It goes without saying, the world is imperfect. In any case, nothing can be done about this. Moving on…

But what are bias and variance, really?

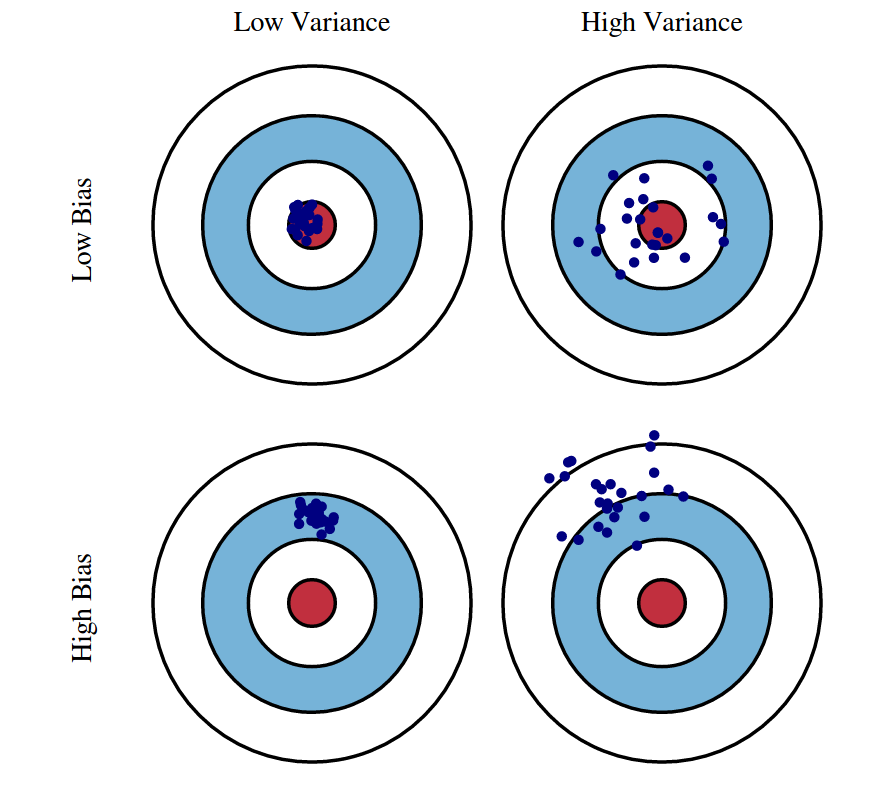
Visualization of the combinations of high and low bias and variance — **Figure 1** - Bias & Variance shown by data points on target

The illustration shows that an optimal model (top left) with low bias and low variance makes highly accurate predictions.
An overfit model (top right) with low bias and high variance reliably predicts data within the data’s mean values as a whole, but with a large difference between predicted and actual output on an individual basis.
On the other hand, is underfit model (bottom left) has high bias, low variance. It creates reliable and repeatable individual predictions, but as a whole are far off the actual data’s mean values.
With a high variance, high bias model (bottom right) is just totally wrong. Begin anew.
Image source: https://scott.fortmann-roe.com/docs/BiasVariance.html

What do underfit and overfit mean, really?

**Figure 2** - Representations of various ML models trained to the same data.
Image source: https://towardsdatascience.com/understanding-the-bias-variance-tradeoff-165e6942b229

In Figure 2 we see an overfit model (left) where the curve of the prediction line is excessively dependent on the precise dataset it is trained on. This proves a unreliable prediction method once data outside the training set is tested against this curve. The prediction made by the model will result in a high degree of variance between the prediction and the reality of the new data. This overfit model corresponds to Figure 1, top right.

Next we see an underfit model (center) which predicts linearly though the data obviously curves. The error of the underfit model stems from the specific model choice implemented (in this case, constant linear) . This biased model corresponds to Figure 1, bottom left.

Finally we find an optimal model (right) that recognizes the curve of the data and finds a generalized mean that minimizes the overall distance between the data and the prediction. This corresponds to Figure 1, top left. The optimal, low bias, low variance model successfully navigates the Bias-Variance Tradeoff, which is our goal.

The optimal model minimizes the Total Error

**Figure 4** - Graphing Bias^2, Variance, and their sum (plus Noise), Total Error, as a function of model complexity in terms of error.

As we have seen above, an overfit model responds to the variation in the data with a complex curve that in the end fails to predict well for new data, whereas an underfit model’s simple curve does little to capture the data variation at all.
We want to find some medium point of model complexity that avoids these extremes. So, as **Figure 4** shows, we find the optimal model complexity where we minimize the total error, being the lowest possible sum of Variance + Bias^2 + Noise.
Image source: https://scott.fortmann-roe.com/docs/BiasVariance.html

Recognizing if bias or variance is your issue

**Figure 3** - The Tell. Are we in Regime #1 or Regime #2?
Image source: https://www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote12.html

So if your artificial intelligence or machine learning model is returning some unacceptable level of error, how do you know if the model is underfit or overfit? Should you solve for bias or variance?

Figure 3 above visualizes and compares the error rates of a model’s output based on both training data and the test data in relation to some pre-defined acceptable level of test error. There are two locations of interest: Regime #1 which indicates an overfit, high variance model and Regime #2 which indicates an underfit, biased model.

We recognize Regime #1 as overfit because while the total error of the model in predicting the output of the training dataset is within bounds of our acceptable test error threshold, the error of the model when predicting the output of the test data is far outside the bounds of acceptable error. The wide discrepency in error rate between a passing training dataset and a failing test dataset indicates the model too closely follows the idiosyncrasies of the training dataset, is thus overfit, and therefore the test error is due to high variance with the model.

In contrast, Regime #2 indicates an underfit model. There is a much smaller difference between the predictions of the test and training set. The model produces consistent answers, but those answers, irrespective of the dataset, are consistently too full of error. This indicates your model prediction does not follow where the data leads, thus is underfit, and the error is due to the bias of your specific model implementation.

Reducing High Variance

So to recap, if you observe the following when training and testing your artificial intelligence or machine learning model…

Symptoms:

Training error is much lower than test error
Training error is lower than the acceptable error
Test error is above the acceptable error

…then the poor performance of your model is due to overfitting. In which case, you should consider…

Remedies:

Add more training data. Perhaps your training data is too small a sample to draw a generalized conclusion, in which case more data would help smoothen out your prediction curve.
Choose a less complex model. Complex models such as Decision Trees are prone to high variance.
Use a bagging algorithm. This will resample and aggregate the data in a way that can simplify your model complexity.

Reducing High Bias

On the other hand if you observe…

Symptom:

Training error is higher than the acceptable error

…then the poor performance is due to underfitting and you should consider…

Remedies:

Use more complex model (e.g. kernelize, use non-linear models)
Add features
Use a boosting algorithm like CatBoost

Summary

We have seen that bias and variance are sources of model error that are identified by the relationship between your model’s training and test error rates and are each reduced by differing methods. Our goal as data scientists, machine learning and artificial intelligence engineers is to minimize the causes of these error to optimize the fit of our prediction models and to do so requires understanding The Bias-Variance Tradeoff.